Brain Models Built From Timing Devices:
A Procrustean Group of Harmonies."

Revision and Construction Note

This page is being developed from an ( ... ) original version that was published in February of 2010. The original version is fixed; this version is for purposes of revision. As of 1/31/2011, no substantive revisions have been made.

Introduction

Jean Piaget (1896-1980) was a pioneer psychologist of child development. In his "operational" model of intelligence, he established the importance of the algebraic group principle. The principle states that a person's activities often comply with the simple, compact system of rules defined for a mathematical object called a group. Compliance may be exact or approximate.

As a primal example, if a person can move freely in a space (e.g., a space of one, two or three dimensions), the movements of the person's body comply with the rules of an algebraic group. Chiefly, two movements, the second following upon the first, are equivalent in effect to a single movement; and any movement can be reversed, returning the body to the point of origin. The rules apply to movements of persons on a soccer field or walking along a street. They also apply to rotations of a wheel around an axis and to arithmetic.

The algebraic group principle organizes movements of other persons' bodies the same as one's own. In The Child's Construction of Reality (1937), Piaget shows how, in the first two years of life, each of us follows a path of intellectual development that leads toward such means of organization. Because the algebraic group principle is universal among persons, it supports objectivity and social order. "This organization of reality occurs, as we shall see, to the extent that the self is freed from itself by finding itself and so assigns itself a place as a thing among things, an event among events." Introduction at xiii. See also J. Piaget and B. Inhelder, The Psychology of the Child (1969) at 15-17 ("Space and Time"); H. Gruber and J. Voneche, eds., The Essential Piaget (1995), part VI ("Logico-Mathematical Operations").

Application of the algebraic group principle to the harmonic structure of Western music reveals a striking paradox. The principle applies to "well-tempered" music but only as a result of compromises and distortions involved in the "tempering." Although such music is entirely generated by human intelligence and evokes experience of the "ideal" and aspiration for the "ideal," the structure falls short of the ideal that would be expressed by a perfect algebraic group structure. Standard musical analysis describes the distortions and compromises using terms such as "Pythagorean comma." To make the structure of Western music fit the algebraic group principle, tones must be stretched or squeezed; and formerly pure, smooth harmonies acquire a rough and tense edge. (Classical North Indian music, e.g., ragas, avoids such problems by never modulating, as evidenced by "drone" tambura players who maintain tonic and perfect fifth tones throughout the performance.)

Stretching and squeezing the facts to fit a form is called "Procrustean" after the cruel bandit Procrustes, a figure in ancient Greek mythology who so tortured the limbs of his victims on an iron frame. I use the word to describe the way "natural harmonies" are stretched or squeezed to comply with the algebraic group principle.

This page presents advanced device designs based on "an Ear for Pythagorean harmonics." A series of developmental designs leads up to "full-scale Ears" which detect a complete set of harmonies in a musical scale and which can be used to investigate the mathematical basis of harmonic structure. The result is a tabular analysis of discrepancies as to the group closure principle. (Figure 15.) That principle would require that two harmonic steps, the second following on the first, must be equivalent to a single harmonic step. More than half the harmonic combinations in the table meet this requirement "perfectly" and are represented by a zero discrepancy -- "0." Other combinations result in small discrepancies under 1%; and there are also combinations with large discrepancies of over 3%.

[In terms of what we hear, a wobbly "beat" heard as roughness is generated by the simultaneous sounding of two tones that are very close. The "beat frequency" is the difference between the frequencies of the two underlying tones. If the beat frequency becomes "sufficiently" low, it is not heard and the two tones seem to be in "unison." In the Ears, such "sufficiency" is adjustable. A human violin player is especially well-trained to detect such roughness by ear, e.g., between his playing and that of his neighbors in the orchestra, and to adjust the position of his fingers on the strings to remove the discrepancy. In addition, there is vibrato, a quivering tone that results from a finger rocking back and forth; vibrato, like love, covers a multitude of sins.]

The fit between the constructed system of harmonies and the algebraic group principle is close but imperfect. I conjecture that the Ears, constructed by means of a subtraction principle, operate as an approximator to a logarithmic function, thus turning addition into multiplication and subtraction into division and ratios. If the fit were exact, a perfect algebraic group would have been established. However, the numbers don't quite work out...

...: link to web page and technical paper setting forth the foundational "Ear for Pythagorean harmonics." This page requires familiarity with the prior presentation.

   

Figure 13:  Table of gaps in group closure for harmonic combinations
(results from the first device design, using a pure tone approximation)

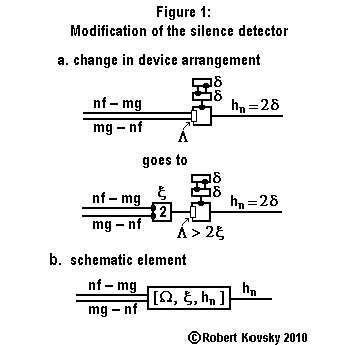
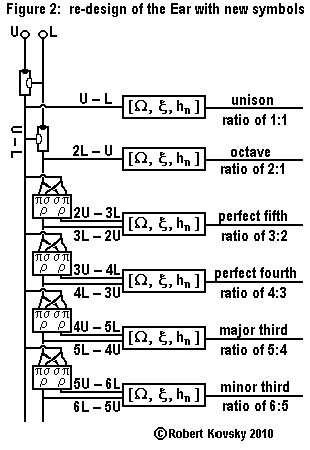
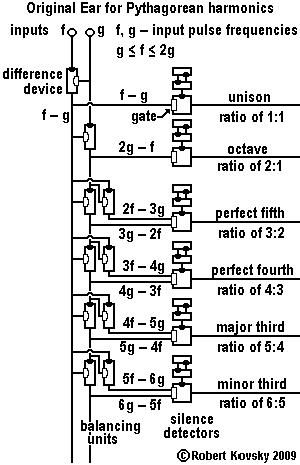
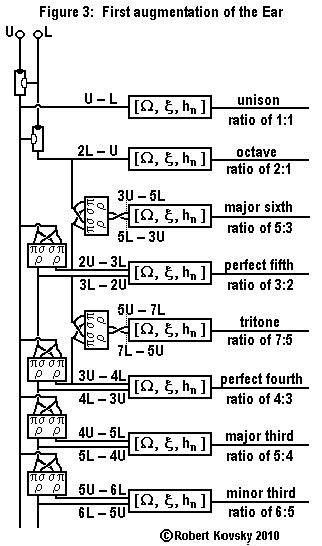
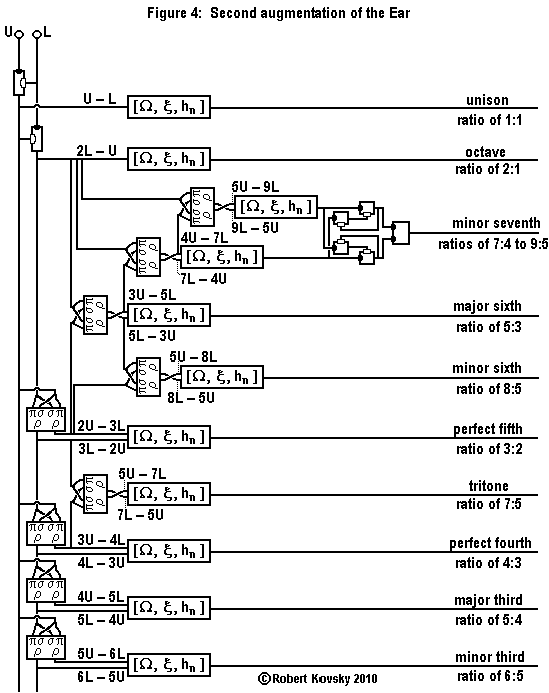
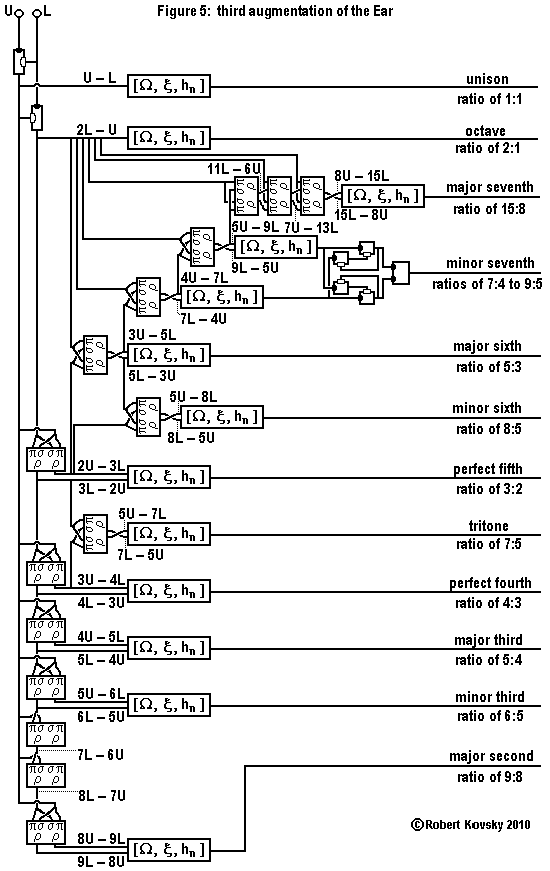
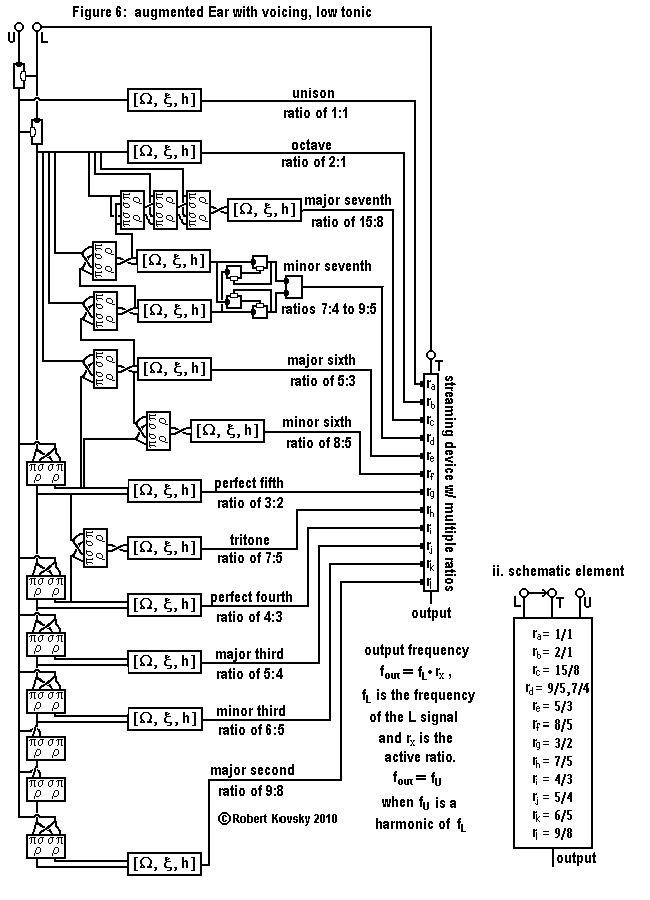
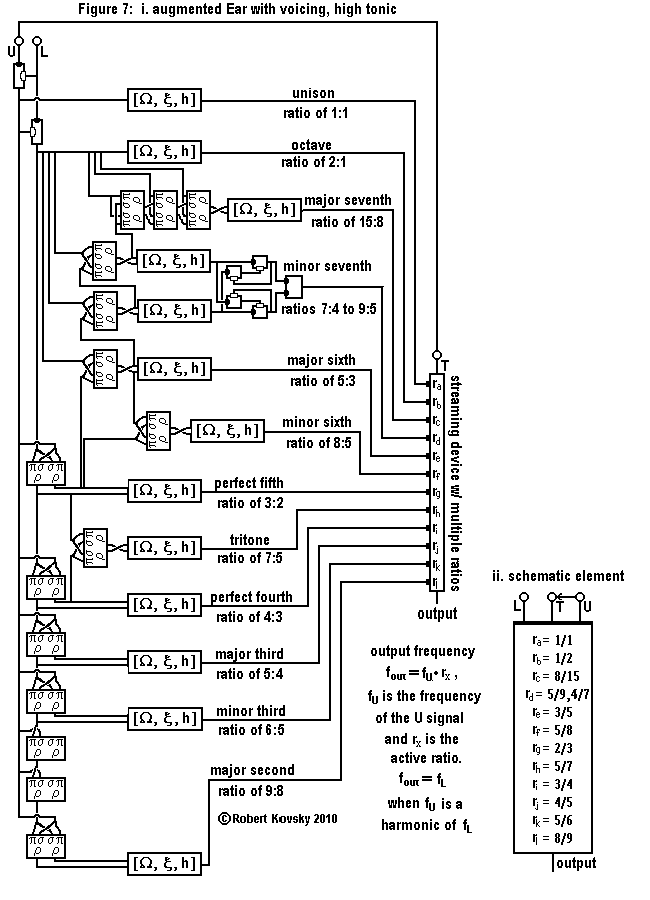
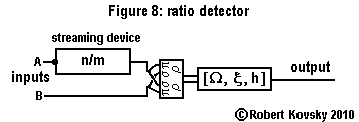
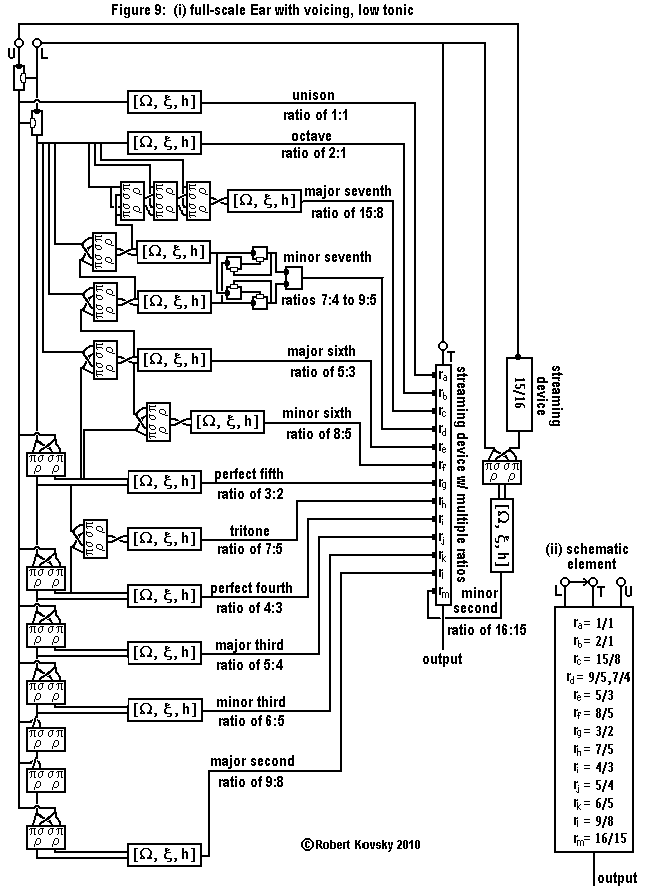
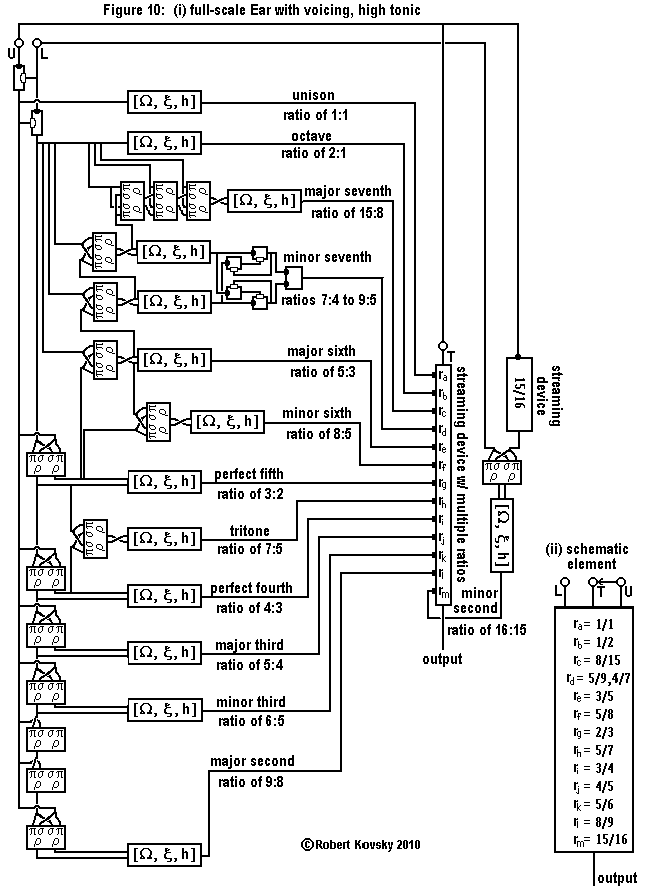
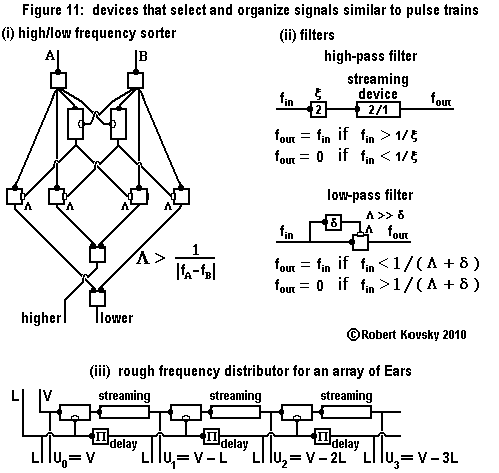
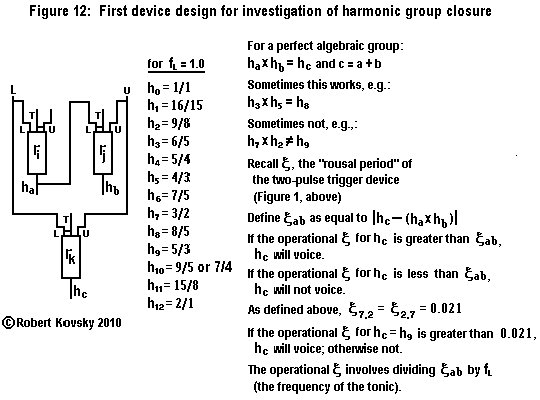
Table of limit values for
ξab = | hc - (ha x hb) |, where c = a + b and (ha x hb) < 2.
index   || 0 1 2 3 4 5 6 7 8 9 10 11 12
   hindex || 1 16/15 9/8 6/5 5/4 4/3 7/5 3/2 8/5 5/3 7/4
9/5 		15/8 2
— — — — — — — — — — — — — — — — — — — 
0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0
1 16/15 | 0 0.013 0 0.030 0 0.022 0.007 0 0.040 0.023 0.008 0  
2 9/8 | 0 0 0.016 0.017 0.006 0 0.025 0.021 0 0      
3 6/5 | 0 0.030 0.017 0.040 0 0 0.013 0 0.045 0      
4 5/4 | 0 0 0.006 0 0.038 0 0 0 0        
5 4/3 | 0 0.022 0 0 0 0.023 0.008 0          
6 7/5 | 0 0.007 0.025 0.013 0 0.008 0.040            
7 3/2 | 0 0 0.021 0 0 0              
8 8/5 | 0 0.040 0 0.045 0                
9 5/3 | 0 0.023 0 0                  
10 7/4
9/5 		| 0 0.008                      
11 15/8 | 0 0                      
12 2 | 0                        

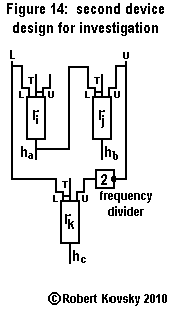
Figure 15:  Table of gaps in group closure for harmonic combinations
(combining results from both device designs and using a pure tone approximation)

Combined table of values for
ξab = | hc - (ha x hb) |, where c = a + b and (ha x hb) < 2; and
ξab = | hc - ½ (ha x hb) |, where c = a + b and (ha x hb) > 2.
index   || 0 1 2 3 4 5 6 7 8 9 10 11 12
   hindex || 1 16/15 9/8 6/5 5/4 4/3 7/5 3/2 8/5 5/3 7/4
9/5 		15/8 2
— — — — — — — — — — — — — — — — — — — 
0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0
1 16/15 | 0 0.013 0 0.030 0 0.022 0.007 0 0.040 0.023 0.008 0 0
2 9/8 | 0 0 0.016 0.017 0.006 0 0.025 0.021 0 0 0.012 0.012 0
3 6/5 | 0 0.030 0.017 0.040 0 0 0.013 0 0.045 0 0.013 0 0
4 5/4 | 0 0 0.006 0 0.038 0 0 0 0 0.025 0 0.028 0
5 4/3 | 0 0.022 0 0 0 0.023 0.008 0 0 0.014 0 0 0
6 7/5 | 0 0.007 0.025 0.013 0 0.008 0.040 0.017 0.005 0.033 0.010 0.021 0
7 3/2 | 0 0 0.021 0 0 0 0.017 0 0 0 0.017 0.006 0
8 8/5 | 0 0.040 0 0.045 0 0 0.005 0 0.030 0 0 0 0
9 5/3 | 0 0.023 0 0 0.025 0.014 0.033 0 0 0.011 0 0.038 0
10 7/4
9/5 		| 0 0.008 0.012 0.013 0 0 0.010 0.017 0 0 0.020 0.021 0
11 15/8 | 0 0 0.012 0 0.028 0 0.021 0.006 0 0.038 0.021 0.008 0
12 2 | 0 0 0 0 0 0 0 0 0 0 0 0 0

Site Links

"Brain Models Built From Timing Devices"

( ... ) Opening Page
( ... ) A Kit of Parts
( ... ) An Eye for Sharp Contrast
    ( ... ) Eyes That Look at Objects
( ... ) An Ear for Pythagorean Harmonics
    ( ... ) A Procrustean Group of Harmonies
( ... ) Fundamentals of Timing Devices
( ... ) Author & History

Related Materials

( ... ) Quad Nets
( ... ) Testimony of Freedom (current long-range project)
( ... ) Embodiment of Freedom (archives of development)

Your comments and suggestions are welcome.
Please write to the adjacent email address (shown in an image to minimize spam).

2/3/11

Copyright © 2011 Robert Kovsky