RIDJGUID

GUIDE TO RIDGE ROUTE

Ridge Route involves a series of devices, realizable on electronics hardware.
The first device is simple and each device builds on its predecessor.
Each device interprets a notation developed in Water Trail.
The interpretative capacities of each device are explored through particular problems.
Device operations can be emulated on conventional computers, but the logic is different. These devices look for "n or more units," while Boolean operations look for "exactly n" units. A combinatorial explosion requires a rapidly growing number of Boolean operation to duplicate a single step command on larger data fields.

Details on author's claim to originality

--device_0

Hardware
associative memory using resistance network
Interpretation
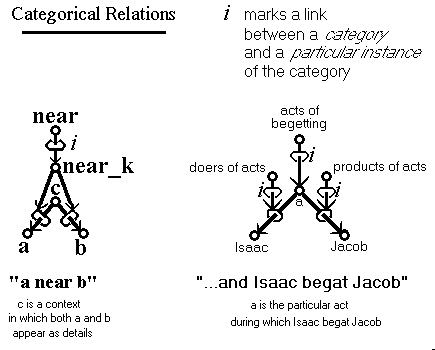
locations ("contexts" and "details") and structural events (ordered pairs of contexts and details)
Commands
steps that count links in forward or reverse
Problems
cases, keywords and keynumbers in legal research

--device_1

Hardware
diagonal access to data; switch bank that holds and transfers results
Interpretation
Unifying contexts and details
Commands
exploring and organizing structures from within
Problems
thesaurus, clusters of references in legal materials, database search tools

--device_2

Hardware
a network involving two device_0 and/or device_1 systems, two switch banks and transfers between devices and switch banks
Interpretation
structural events become locations
Commands
organizing and controlling structures through forms
Problems
website design, language representation, stored programs

--device_3 (matters for further investigation)

Hardware
interwoven negative (inhibitory) system; variations in connection strengths
Interpretation
exclusions; differentials (e.g., rating on a scale 1 to 7); covariance and co-ordination
Commands
organizing and controlling structures through variations in device operation
Problems
cluster problems; reciprocal and interactive imagery

--device_4 (anticipations and speculations)

Hardware
replace clocked steps with separate pulsing emitters and command structure that calculates activity based on device history
Interpretation
locations become foci of activity that collectively excite and inhibit each other
Commands
measuring and controlling stabilization parameters; interfaces
Problems
spaces; activity-based schemata; robotics

All materials copyright by Robert Kovsky, 1997.

MY CLAIM TO AN ORIGINAL DESIGN

Theories about "associations" pre-date electronic computers. Anderson & Rosenfeld, eds., Neurocomputing: Foundations of Research (1988). Investigators have studied many devices emphasizing network connectivity. I have looked at the literature and have not uncovered anything similar to my approach.

In contrast to other approaches:

The Hopfield model and its descendants do not figure in my work [See Hertz, Krogh & Palmer, Introduction to the Theory of Neural Computation (1991)];
I see pattern recognition as part of a more general problem (resolution of ambiguty structures) [Compare to Kohonen, quoted below on another matter];
Problems are encountered at different stages of development: database searches were the first problem addressed in my approach, while some logical functions that are part of the chip design in von Neumann architecture are an end-stage development in my approach;
Non-linear dynamics and speculations about biological neural networks are important (see my speculations in Device_4), but my view is that chemistry is at least as important in brain function as electrical connectivity (and that the interaction between the electrical and chemical components is the driving force).

My claim to originality is most clearly stated in the notational extension that removes the distinction between a node and a link. This extension is realized on devices I have designed.

The event (link plus nodes) becomes a location (node) (Device_2).

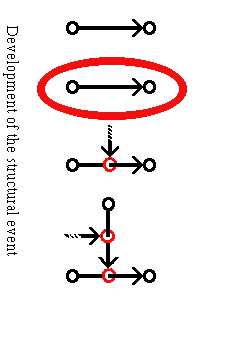
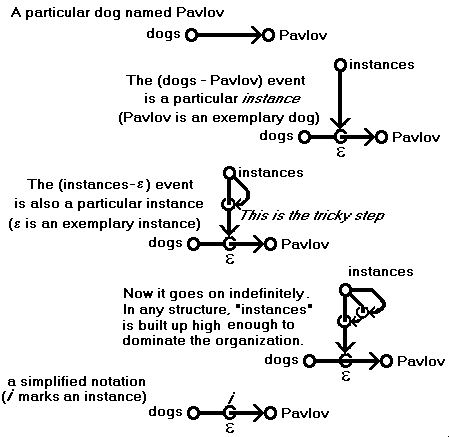Instance relations follow from the extension.

Applications to language representation

In Self-Organization and Associative Memory, (1984) at 27 and 29, Prof. Teuvo Kohonen states:

Relations."A linguistic relation between two expressions x and y is defined, for instance, by a statement of the type 'the attribute R of object x is y' ... Sometimes a notation is used for the simplest type of relation which is then read 'x is related to y by R'. In this case x and R consist of finite sets of discrete values (words or clauses) so that if the format of this statement is fixed, symbolically it is defined by an ordered triple (R, x, y). Variables in the ordered triple are often given the particular meanings A = 'attribute', O = 'object', and V = 'value'. An expression (A, O, V) is then read 'the A of O is V'. ...
On the Interpretation of Relations as Associations. Are the relations and associations one and the same thing? The question needs closer examination. Consider the following types of claims that occur in the literature [references omitted]: 'An association is a two termed relation, involving three symbols, one of which names the relation, the other two arguments'; 'a relation consists of three components, an ordered pair of items and a link which specifies the type of association which relates items'; and 'an association is an ordered triple (A, O, V) of items ... called the components of the association'. What has been said above is essentially that a relation is thought to link the terms O and V, or that all components in a triple (A, O, V) are mutually linked. Apparently A cannot be understood as a simple link because it contains the representation for a label; a more expedient view might be that all elements A, O, V that have been stored together in this specific order are associated. " (emphasis added)

Relations based on the extension illustrated above are clearly different from the relational notations described by Prof. Kohonen.

Another perspective on the originality claim: Mathematical note to Device_2

Return to top of this page