-- Guide to Ridge Route

DEVICE_4

Activities become primary parameters

Developing activity

remove

synchronous inputs and outputs -- through which structural events are explored with a mass action step -- controlled by an external clock -- the design introduced in device_1

replace with

new input/output hardware with a parameter of activity (e.g. frequency, or pulses per second) -- calculated on the basis of the history of that location's activity and of the activity history of locations connected to the subject location through structural events. Calculations are effected through convolution (superimposition) integration carried out by conventional computer chip at each location.

The nature of on_locations is also changed. Previously, on_locations were distinguished from other locations. Now, all locations are on_locations, but they differ in activity. Those with higher activity are more brightly on.

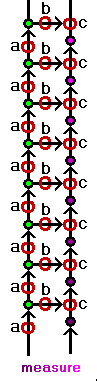
Developmental principles advise that device_4 should "reduce" to earlier devices:

• As the accompanying image suggests, it may be possible to connect activity-based devices in ways that result in conditions of state
• In the adjacent image, the letters "a," "b," and "c" mark fixed values for activity parameters that control the pattern. The purple kind displays a useful variation in activity, especially if the pattern is stable, montonic, perhaps even linear. The green kind are also determined by a, b and c, but are only incidental.
• Stable patterns of activity (like measure) would allow for the construction of structural forms that can be used for self-organization of locations, thus extending regions of stability. Hypothetically, it may be possible to define formulas used in the convolution integration to reach this result.
• Sequential patterns of co-ordinated activity -- perhaps resembling Piaget's schemata -- may also be worth investigating in a similar manner. Co-ordination means that a stable pattern in one area of a device leads to an instability in another area; when the second area re-stabilizes, the first is thereby de-stabilized; and there is an orderly succession of stabilizations and de-stabilizations.
• Externally imposed signals that give rise to stable input patterns may stablize activity in regions of the device. Device operations would resemble natural experience where external things achieve their presumptive reality by appearing permanent and coherently integrated with other reals. Such external things become forms onto which multiple faculties of experience (and the experience of different persons) can adapt conformingly and integrate thereon. Forms give rise to interfaces between different faculties of experience (e.g., hand and eye co-ordinating through common structures of space and time) or between different persons. Piaget's approach recommends material objects, space, time, motion and causality as early candidates for device interpretation.
• One approach to exclusion relations is a structure that can establish several stable patterns, but, of course, only one at a time. It is also possible that a stable pattern in one region stablizes another region, leading to active evolution of stable patterns of activity according to exclusionary relations. (Like domino designs where each falling domino strikes down another one or more and where the paths collapse predictably.)
• Operations in device_4 should be able to mimic the action of previous devices. In other words, there should exist designs and command structures that yield the same results as corresponding designs and command structures according to device_0, etc. The reportoire of the new device should include the reportoire of previous devices, as well as include new possibilities not previously available.
• Calculations might be in the form of difference equations. That is, a location's next value for activity will be calculated from past values of its activity and/or (through structural connections) from past values of activity of other locations. Some examples are ovbvious, e.g., forward step on device_0 is a summation. In the long run, though, difference equations are notioriously intractable mathematically. See, e.g, E. A. Jackson, Perspectives on nonlinear dynamics, chap. 4.
• The author anticipates that development, if it is to occur, will require the building and testing of actual devices that allow an experimenter to modify values and convolution terms and observe the results directly.

The author's approach to device_4 is guided by scientific approaches to large-scale physical systems.

• Statistical mechanics deals with physical systems made up of a multitude of interacting material elements, but of only a few kinds. E.g., a mixture of gases in a piston-and-cylinder device. Statistical mechanics has been applied to network problems. Hertz, Krogh & Palmer, Introduction to the Theory of Neural Computing (1991).
• Statistical mechanics is properly defined only for a system in equilibrium -- when all overall characteristics have stopped changing. Although some progress has been made in extending the reach of its methods into non-equilibrium conditions (e.g., the Onsager relations in physical chemistry), statistical mechanics cannot be applied to systems characterized by values that are always changing as a result of externally applied inputs and unpredictable combinations of signals generated internally.
• One suggestive area of statistical mechanics involves materials existing in multiple phases, such as liquid water and vapor water (steam). J. Willard Gibbs, a principal founder of statistical mechanics, derived the Gibbs phase rule that relates degrees of freedom directly to the number of substances present in a physical system at equilibrium. There are analogies between the phase rule and the mathematical theory of connectivity. The structures of ideas and the meanings themselves are particularly apropos to the author's point of view.
• The mathematics of "chaos" and "complexity" are suggestive of some physical processes. In The Origins of Order (1993) 29-30, Stuart A. Kauffman argued for a mathematical approach to questions about the evolution of biological species and concluded that:

  "complex systems" poised on the boundary between order and chaos [may be] the ones best able to adapt by mutation and selection... Such systems, it begins to appear, harbor behavior which is the most flexible, complex and adaptable. If so, we may have uncovered a universal in biology...

  Prof. Kauffman's characteristics (flexible, complex and adaptable) would also be descriptive of freedom.
• There are models that use the mathematical boundary between order and chaos to account for behavior of materials at or near changes in phase. The mathematics suggests that at or near the boundary, instabilities can appear, such as the turbulence in water boiling at 100 degrees Celsius. We can control the fact of turbulence easily, but the details only partially. Controlled instability may be useful in the nervous system of an animal that must quickly take advantage of opportunities and avoid risks. Speed must be achieved, even at the cost of error.
• Some researchers suggest that brains maintain chaotic conditions as part of their functioning. E.g., Skarda & Freeman, "How brains make chaos in order to make sense of the world," Behavioral and Brain Sciences (1987) 10, 161-195. The authors studied signals generated by the olfactory bulb of rabbits and concluded that they were able to identify patterns of activity corresponding to discrimination in smell. Measurements of electrical signals indicated that during inhalation, the rabbit's olfactory bulb becomes energized and enters into a chaotic condition.

  Order emerges from the chaos... the local amplitudes of oscillation take on values that are reproducibly related to particular odorants... The values differ for different odors, indicating that multiple limit cycles exist, one for each odorant an animal has learned to discriminate behaviorally... (p. 168)

• Piaget explored these issues throughout his career. See, e.g., Biology and Knowledge, (1967), especially chapter 7, with portions reprinted as selections 45-47 in Gruber & Vonèche, eds., The Essential Piaget (2nd. ed. 1995):

  Thus, the fundamental reality about living things is constituted neither by timeless structures, standing outside history or dominating it like equilibrated organization forms with permanent conditions, nor by a historical succession of chances or crises like a series of disequilibria without equilibrations. It consists, rather, of continuous processes of autoregulation implying both disequilibria and a constant equilibration dynamism... ...we find the simultaneous intervention of exogenous factors, causing disequilibria but also setting off "responses", and endogenous factors, producing these responses and acting as equilibration agents.

  (emphasis added)

The author envisions a device designed to maintain patterns of activity near the boundary between order and chaos and that might resemble conceivable designs for a brain.

• It is expected that difference equations used to calculate activities can be written and adjusted (in practice or in emulation) so that the patterns of activity are borderline chaotic.
• The equations might take a form modelling a physical system made up of two interacting parts, e.g., an electrical network operating in a chemically rich environment. The physical system could be divided into regions, each characterized by particular parameters governing the electrical operations and species of chemicals. Intense, chaotic activity of the electrical system might cause an increase in populations of chemicals that quiet activity, while a generally quiet electrical system might cause an increase in populations of chemicals that excite activity. It is possible to conceive of physically distant regions reciprocally interacting and mutually stabilizing on a single pattern. Successive mutual stabilizations might constitute co-ordination.
• Such a system would, by its nature, be a heavy consumer of energy. One should expect such a system (or a model based on it) to incorporate a gross limit to energy consumption. Such a limit would be like a leash that allows aggregate activity (according to an appropriate measure) to approach but not exceed a defined value.
• The defined value, like the length of a leash, could be adjustable and could be set so that the system can initially sustain only borderline instability. Once an instability was established in a region, however, the leash could be adjusted to let it grow. There might be a separate leash for each region and a global leash.
• Such a system might sustain a connected region of borderline instability in a matrix of stable patterns. A sustained region of borderline instability might become unstable after a fragile binding to a basin of attraction was broken by an outside influence that had only a slight energy content. Re-stabilization might recur under different conditions, e.g. running fast instead of sitting and waiting.

The author envisions interpretating an instability in a device as an ambiguity in a data structure.

• Device_4 can be alternatively viewed as a collection of systems sharing features or as different systems participating in interfaces with one another.
• Interfaces incorporate stable regions.
• Instability and stability interact when, through device operations, portions of an unstable region become stable or portions of a stable region become unstable . Regions of stability and instability evolve together while involving inputs from external sources.
• In stage 5 of Water Trail (no substance presently available), the author contemplates constructing ambiguities by superimposition of structures partially incongruent (they fit together only imperfectly).
• The author envisions correspondences between ambiguities in data structures and instabilities in interfaces within a device. An ambiguity arise from a superimposition of structures where there is a conflict between features (that can be related through exclusions). Superimposition without conflict can be part of a contextual matrix. The superimposition corresponds to interface, the matrix corresponds to stability, and the ambiguity corresponds to instability.
• Ambiguities are resolved by the evolution of structures and evolved structures often generate more ambiguity. (This is the history of juridical law).
• One model is that of a judge presented with isolated issues -- conflicting versions of events or law -- but where everyone is agreed about the context and most of the details. The judge generally has discretion, or freedom of choice within the law, in connection with those issues. That's why the conflicts are important -- they direct the attention of the participants and their resolution determines the outcome.
• Once ambiguities have been resolved, they cease to require attention; and everyone moves on to something else.
• Ambiguity and structure, instability and stability -- perhaps even consciousness and memory -- embrace, penetrate and change each other. The patterns are forever new and forever unpredictable. We chase through them, chase ourselves, running from anxiety and toward illusion.

  Yet, they are, they must be patterns of something real. Their evident utility for the sustenance of life, as well as the many comforts and pleasures they provide us, awakens and confirms the certainty that the patterns attach to something real and that we can climb on them and through them. Climbing is risky, but success brings joy. With further good fortune and auspicious constraints, it may be possible to develop a technology of freedom.

All materials copyright by Robert Kovsky, 1997.