Brain Models Built From Timing Devices:
An Ear for Pythagorean Harmonics

Timing devices" is a new approach to brain science, based on a new technology.

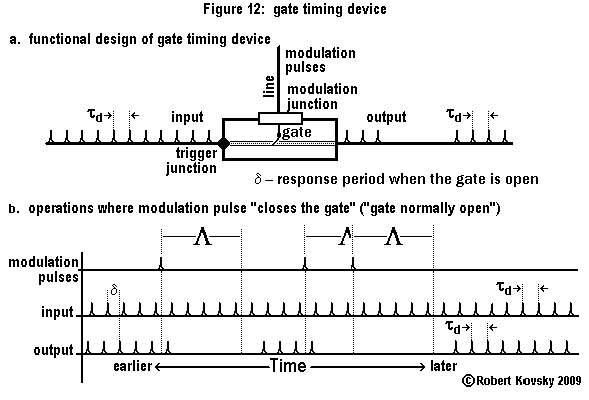
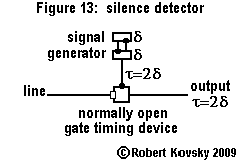
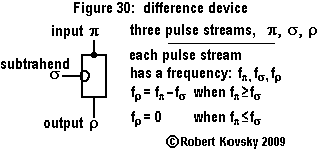
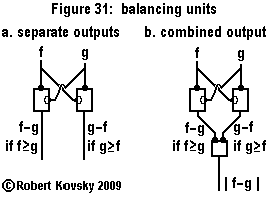
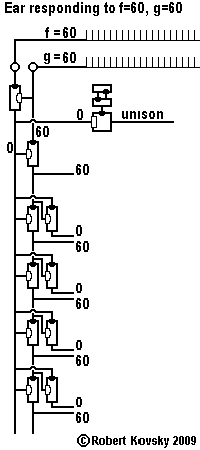
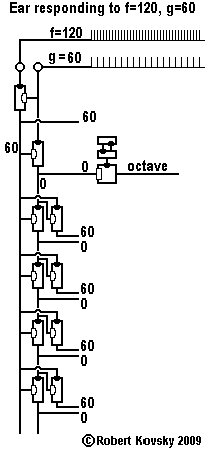
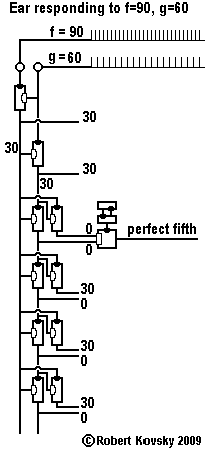
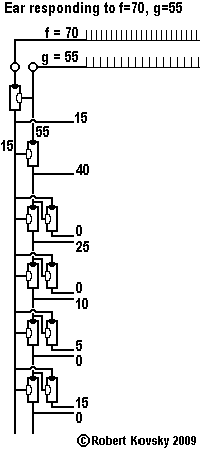
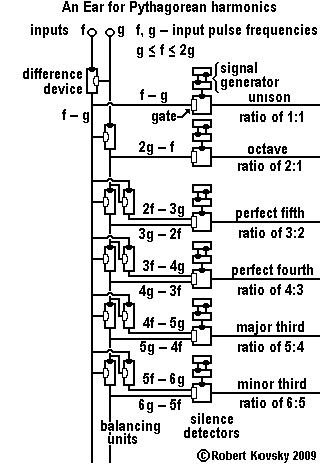
An Ear for Pythagorean harmonics is a device design that shows how timing devices can imitate brain functions. The design for the Ear is shown in the adjacent image and discussed on this page.

In operation, the Ear detects when two input signals f and g, "pure tones" musically, are in a relationship that is known as a "Pythagorean harmonic" (octave, perfect fifth, major third, etc.). When a harmonic relationship is detected, a signal appears on the output line bearing the name of the harmonic. A frequency combination shown on an internal line, e.g., 3g – 2f, is operative when the relationship is close to the associated Pythagorean harmonic, e.g., close to 3g – 2f = 0 or f = (3/2) g, which is the "perfect fifth" relationship.

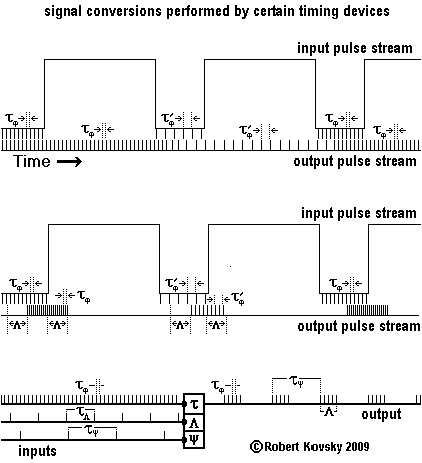
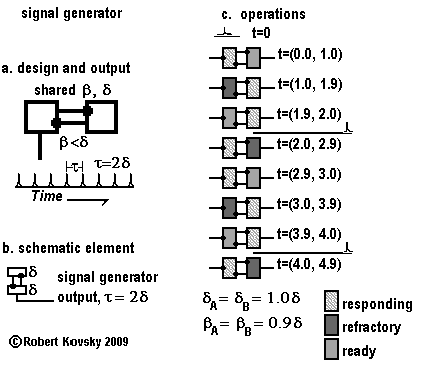
The timing devices system has many resemblances to "standard electronic circuits" built from resistances, capacitances, transistors, etc. In both technologies, components belong to a "kit of parts" and are assembled to perform specific functions. However, timing device components are different from standard electronic circuit components and the signals are also different.

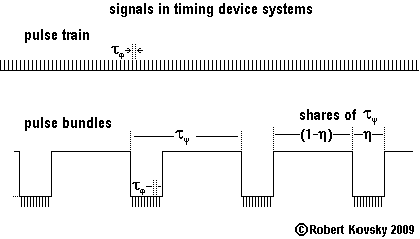
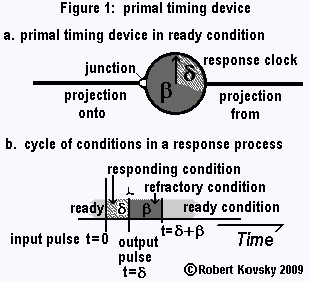
Timing devices also resemble neurons. Timing device signals are like the signals that travel on nerves -- a stream of "spikes" or "action potentials," which are instantaneous packets of energy -- called "pulses" in the timing devices system.

A technical paper, ( ... ) "An Ear for Pythagorean Harmonics," is available for download, a .pdf file, 561 kB. The technical paper presented the timing devices system at a certain stage of development that occurred about New Year of 2010. It has substantial material not otherwise available on the site. Development of the timing devices system has progressed since the Harmonics paper was written. For example, the difference device has been re-constructed conceptually in ( ... ) Fundamentals of Timing Devices, although operations remain the same. The original paper has not been revised other than a correction to Figure 45.

This page offers a reduced presentation of the Ear and the timing devices system. The reduced presentation is simpler than the ( ... )  Kit of Parts presentation. Some text materials and numbered figures are copied from the technical paper.

This web page is a revision of the ( ... ) original version that was published in February of 2010. The original version is fixed; this version is subject to change as part of the larger, ongoing project, Brain Models Built From Timing Devices. Please see the ( ... ) links list.

Contents of this page:

...  Signals in Timing Device Systems
...  Timing Device Components and Units Used in the Ear for Pythagorean harmonics
...  Primal Timing Device
...  Signal Generator
...  Gate Timing Device
...  Silence Detector
...  Difference Device
...  Balancing Unit
...  The Pythagorean Harmonics and Operations of the Ear

...  Links to Related Works by the Author

Signals in Timing Device Systems

Signals in timing device systems are made up of pulses and pulse patterns. There are also "periods between pulses," where a period is the amount of time from one pulse to the next.

A "pulse" is an idealized version of an "action potential" or "neuronal spike" seen in nerve cells.

The two chief types of signals in timing device systems are shown in the adjacent image: uniform pulse train and pulse bundles.

Some timing devices operate with pulse trains and other timing devices operate with pulse bundles. Certain timing devices convert signals from one form to another. The adjacent image shows three examples of conversion. The top two images show inputs and outputs of two kinds of "streaming devices" and the bottom image shows inputs and output of a "pulse bundle generator." (Please see Figures 26, 28 and 29, respectively, in the technical Timing Devices paper.)
Return to contents.

Timing Device Components and Units Used in the Ear

Primal Timing Device

The "primal timing device" models a very simple brain cell (neuron) and is the point of origin for development of more complex timing devices. Operations of the primal timing device are minimal. The arrival of a pulse at the primal timing device starts a process that leads to the discharge of a pulse from the primal timing device, after a period of time. After discharging the pulse, the primal timing device is unresponsive for another period of time.

The primal timing device has a "response clock" that is like a stopwatch used in sports contests, shown in Figure 1.a as a circular clock dial. Two projections connect the primal timing device to other timing devices and a junction connects the "projection onto" to the response clock. A pulse arriving at the junction through the projection onto starts the "response process," which runs through a cycle of conditions, during which the primal timing device discharges a pulse through the "projection from."

As shown in Fig. 1.b, a primal timing device has a "ready condition," a "responding condition" and a "refractory condition." The device responds to an arriving input pulse only when it is in the ready condition. Suppose an input pulse reaches a ready device at time t = 0, initiating the response process. The response clock starts and the device enters into the responding condition. At t = δ, the device discharges an output pulse through the projection from; and the device enters into the refractory condition, which continues until t = δ + β, when the device enters into the ready condition, completing the response process.

Return to contents.

Signal Generator

Two inter-connected primal timing devices function as a signal generator, as shown in the adjacent images. Image a shows the design and output of the signal generator. The design resembles that of a multivibrator in standard electronic circuits. Image b shows a schematic element that is used in the design of the Ear for Pythagorean harmonics.

Image c shows the signal generator in operation. An initiating pulse arrives at time t=0. Thereafter, the assembly goes through changes in an orderly way, represented by a sequence of momentary images, like frames in a video. Conditions of timing devices last for a specified period of time stated as t=(a, b) in each momentary image. In the idealized operations of timing devices, conditions change instantaneously. The images show conditions "before" and "after" each change; but the changes themselves are not shown. However, the discharging of pulses is pictured as taking place during changes that occur at t=2δ and t=4δ.
Return to contents.

Gate Timing Device

Figure 12 shows a "gate timing device." It has functional parallels to conventional electrical and electronic circuit components that have the nature of "gates" or "valves" - e.g., electrical relays, vacuum tube triodes and "npn" transistors - but with a new kind of signal and operations.

As shown in Fig. 12.a, a gate timing device has two different junctions. The "input" projection onto and the "trigger junction" have the same function and operations as in the primal timing device. In addition, a second projection onto the timing device, called the "line" in Figure 12, attaches through a different kind of junction, called a "modulation junction." "Modulation pulses" are carried through the line onto the modulation junction.

Figure 12.b shows the operations of the "gate normally open" gate timing device. An input pulse leads to a primal, delayed output pulse when "the gate is open" but the output is silent when "the gate is closed." A modulation pulse closes the gate for a period of Λ, the "modulation period." The gate is closed as to input pulses arriving after the arrival of the modulation pulse; there is no interruption of a response process initiated prior to the arrival of the modulation pulse.

If a modulation pulse arrives while the gate is closed, the gate will remain closed for Λ additional seconds, or longer, if more modulation pulses arrive. If modulation pulses arrive at a frequency greater than 1/Λ, the gate will be maintained in a closed condition.

Return to contents.

Silence Detector

Figure 13 shows the design for the silence detector that is used in the Ear for Pythagorean harmonics. The silence detector is assembled from a signal generator and a normally-open gate timing device.

In the silence detector, the normal condition of the gate timing device corresponds to silence on the line to the gate. When there is such silence, the gate is open and the signal from the signal generator passes through to the output.

On the other hand, when pulses arrive regularly through the line onto the modulation junction of the gate, the gate will stay closed. Then there is no output.

In brief: a signal on the line means a silent output. Silence on the line means that a signal from the signal generator appears as the output of the silence detector.

In idealized operations, inputs to the Ear are very long pulse trains, each pulse train specified by the period between any two pulses. The value of Λ in the gate timing device is also very large so that many pulses from the signal generator are blocked off by each modulation pulse and the modulation pulse frequency needed to keep the output silent is relatively small.

Return to contents.

Difference Device

Figure 30 shows the design element for the difference device and its operations as a frequency subtraction device.

There are three signals: pulse streams π, σ and ρ. Pulse stream π is the input to the difference device. Pulse stream σ - called the "subtrahend" - resembles the stream of modulation pulses to the gate timing device but with somewhat different effect. Here, each pulse in the subtrahend stream cancels one pulse from the input stream. Pulse stream ρ is the resulting output stream.

Operations require that "defined" pulse streams arrive through the input and subtrahend lines. A defined pulse stream need not be perfectly uniform; it is sufficient if a specific pulse frequency can be assigned and if irregularities  –  "holes" resulting from cancellations  –  are smoothly distributed. These requirements are met for operations of the Ear for Pythagorean harmonics.

A defined pulse stream has a specific frequency and the following relations describe the operations of the device.

fρ = fπ – fσ when fπ > fσ
fρ = 0 when fπ < fσ.
Return to contents.

Balancing Unit

Figure 31 shows an important use of the difference device, in two versions of "balancing units." In each version, two difference devices are hooked up to two pulse streams (f and g) that serve as input and subtrahend, one each to each difference device. For two defined input pulse streams, no more than one difference device will be operating at any given moment and its output line will be carrying a signal; the other difference device will be silent. If the two pulse streams are identical (or nearly so), both lines will be silent.

Figure 31.a shows a balancing unit with separate outputs.

In the balancing unit shown in Figure 31.b, the outputs from the two difference devices are inputs to a simple timing device. At any moment during controlled operations, no more than one difference device generates input to the simple timing device and the simple timing device responds like a primal timing device. The possibilities are combined in the formulation | f–g |, denoting the absolute value of f–g. The same principles apply to output of a balancing unit combined at the gate of a gate timing device, shown in the design of an Ear for Pythagorean harmonics.
Return to contents.

The Pythagorean Harmonics and Operations of the Ear

The Pythagorean Harmonics

Two different musical tones heard together can produce in the listener a pleasant sensation additional to that felt when the two tones are heard separately. Such pleasant sensations, called "harmonies" or "consonances," are a foundation of music. Another pair of tones heard together might give rise to an unpleasant sensation, called "dissonance," which is experienced as a kind of tension.

In a mathematical approach to music, each tone is described by a frequency, sometimes called a "pitch"  –  namely, a certain number of "cycles per second" or Hertz (Hz). A pitch of 440 Hz denotes the sound of a conventionally-tuned violin playing an open A string.

The ancient sage Pythagoras first discovered that consonance between tones can be identified by simple ratios of whole numbers, such as "3:2." Expressed in the modern language of frequencies: when the frequencies of two tones define a simple whole number ratio, the pair of tones gives rise to a pleasant sensation or consonance. A musical scale consists of tones that, taken in pairs, define certain ratios with respect to one another. Simple ratios identify pleasant pairs and complex ratios identify tense pairs. Pleasure and tension are thus identified with ratios (also known as "pitch relations") and ordered accorded to numbers, on the one hand, and a musical scale, on the other hand.

All agree that the starting point is 1:1 or unison. The most pleasant ratio is 2:1, or the octave. Then, ratios are found to be pleasant in order according to a scheme: 3:2 (perfect fifth or dominant); 4:3 (perfect fourth or subdominant); 5:4 (major third or mediant). These five notes and relations make up the essence of a scale. In the Ear for Pythagorean Harmonics, the scale is extended to the ratio 6:5, a minor third.

A chief feature of musical experience is that much the "same" pleasure is aroused by any two tones that are in a specific pitch relation, such as 3:2, regardless of the absolute pitch. E.g., two tones of 600 Hz and 400 Hz, heard together, will arouse much the same experience as 660 Hz and 440 Hz, heard together. Accordingly, a musician can "transpose" one set of pitches in one "key" (tonic and subordinate tones) to another set of pitches in another key and yet reproduce musical feelings of pleasure and tension almost exactly.

"An Ear for Pythagorean harmonics," assembled out of timing devices, suggests a basis for these facts of experience.

Operations of the Ear at the limit points of its range

The full design for the Ear is at the top of the page. In images below, the Ear is reduced to essential operational features for specific cases.

Operations of the Ear depend only on ratios; therefore, it is possible to construct examples with convenient numbers. For examples here, the foundational tone, g, is set equal to 60 Hz, or, simply, g=60.

The operating range of the Ear is defined as: g < f < 2g. For g=60, this means that f can range from f=60 to f=120.

 
The adjacent images show the Ear operating at the limit points of its range of operations. At one limit point of the range of operations, when f=60 and g=60 and the two inputs are "in unison," the Ear detects that fact and a signal appears on the "unison" output line but on no other output line. The image for f=60, g=60 shows only the single silence detector where the gate is open. Its modulation line is silent; the frequency of the signal to the modulation junction is 0.

The other image shows operations at the limit point that is the polar opposite of the first, that is, when f=120 and g=60 and the relationship is "octave." Again, that fact is similarly detected and a signal appears on the "octave" output line but on no other output line.

In each image, the frequencies of the paired outputs of the balancing units at levels below the octave all have the same values. The frequencies of those paired outputs when the inputs are f=60, g=60 are reversed from the pairs when the inputs are f=120, g=60. As f traverses its range, moving from 60 to 120, the paired frequencies shift in an orderly but complex fashion from one extreme to the other.

Operations of the Ear at intermediate points in its range

 
The adjacent images show operations of the Ear at intermediate points in its range of operations.

When f=90, g=60, the relationship between the input tones is that of a "perfect fifth," as detected by the Ear. Both inputs to the perfect fifth silence detector are silent. The ratio is f = (3/2) g.

When f=70, g=55, the relationship between the input tones is not a simple ratio. Rather, the ratio is 14:11. None of the balancing units produces a pair of silences and none of the outputs of the Ear carries a signal. This is an unmusical relationship between a perfect fourth and a major third.

For each of the consonant relations that is shown in the images — unison, octave and perfect fifth — only a single active frequency appears on the internal lines of the Ear. When f=70, g=55, on the other hand, every internal pair is different and many frequencies appear. The principles of the Ear suggest that the many internal frequencies in the latter case identify a source of tension or dissonance in human musical perception, in contrast to conditions during consonance.

(return to top of page).

8.  Link List

Brain Models Built From Timing Devices

( ... ) Opening Page
( ... ) A Kit of Parts
( ... ) An Eye for Sharp Contrast
    ( ... ) Eyes That Look at Objects
( ... ) An Ear for Pythagorean Harmonics
    ( ... ) A Procrustean Group of Harmonies
( ... ) Fundamentals of Timing Devices
( ... ) Author & History

Related Materials

( ... ) Quad Nets
( ... ) Testimony of Freedom (current long-range project)
( ... ) Embodiment of Freedom (archives of development)

Your comments and suggestions are welcome.
Please write to the adjacent email address (shown in an image to minimize spam).

2/26/11

Copyright © 2009, 2010, 2011 Robert Kovsky