Mechanical Metaphors
for Thermal Models of Brains

Thermodynamics, the theoretical basis for Quad Nets (a Thermal Model of Brains), is distinct from Mechanics, the basis for models using differential equations of time evolution and/or models based on computers. However, some mechanical metaphors may provide insight.

1. A mechanical metaphor for cyclical selection in Quad Nets

The images below show a mechanical metaphor for cyclical selection in Quad Nets. A ball is under the continuous vertical influence of the force of gravity, denoted by g. There is also a smaller, varying horizontal influence. The ball is constrained by a surface that changes as time proceeds during a repetitive cycle.

In images i and ii., a small horizontal influence is ineffective to move the ball because it is constrained by a concave-upward surface.

In image iii, a small horizontal influence can move the ball, but there is no sustained result.

Image iv. shows the critical moment during the cycle, when the constraining surface is flat (or nearly so).

At the critical moment, a small horizontal influence determines whether the ball rolls to the left or, as in image iv., to the right. If the surface is changing slowly enough at the critical moment, the rolling is reversible, should the influence reverse in a sustained way.

In image v., the velocity is small and a large leftward influence would be required to reverse the direction, but the possibility is not excluded.

In image vi., the velocity is so large that the direction of motion cannot be reversed. As the cycle proceeds, the velocity grows in magnitude. The system later returns to image i. and a new direction is established by the influence then prevailing.

2. A mechanical metaphor adapted from Calvin's Cerebral Symphony

I use materials from Cerebral Symphony (1990) by neurobiologist William H. Calvin as a focus of discussion.

Calvin's images reproduced below show a model for throwing an object, using a sequence of "modular motor commands" (first image). Note that Calvin identifies a "critical interval" during which the activity is defined. Calvin then extends his proposal to state a metaphoric model (second image) based on a "candelabrum-shaped railroad marshaling yard" with converging "tracks" where mental activity is analogized to constructing and selecting among "trains of thought" and where "there is surely a lot of activity going on there, because they are shuffling and mutating, trying new schemas for both sensory templates and movement programs, creating new sequences." (Cerebral Symphony figures and text at 248 and 262-263.)

As I interpret Calvin, there are large classes of activities that can be described by such modular units. Such activities include keyboard performances that run a span, at the least, from children's toys to a piano to computer programming. These activities all share common features that Calvin's railway metaphor highlights. For purposes here, the most interesting features revolve around the hooks that fasten the metaphorical railway cars together. Metaphorically, hooks that connect railway cars identify a major question about brains.

Hooks between railway cars have two functions that oppose each other and that must be balanced. First, a hook fixes one car to another. Second, a hook allows for assembling and disassembling trains of cars. A heavy hook with a tight-fitting connection is best for permanent fixation, the kind of permanent fixation that will maintain the connection despite twisting and banging on a long journey. For quick assembling and disassembling, on the other hand, the hook should be light in weight and with a loose connection that is easy to slip. In contrast to heavy, tight, fixed hooks good for stressful journeys, hooks good for the inner railway yard are light and mobile.

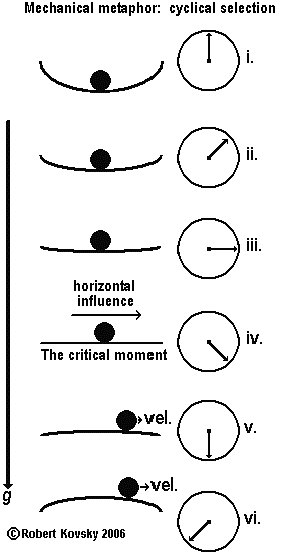
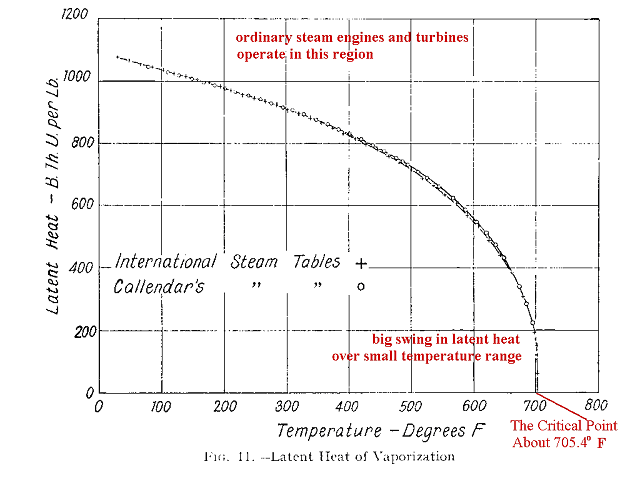
Critical point principles applied to liquid water and steam show how a hook can vary between heavy/tight and light/mobile. At the critical point, liquid water and steam are indistinguishable and merge into a unique state, a kind of indeterminate goopiness where surface tension is zero and blobs of all sizes emerge, merge and dissolve incessantly. Another way of saying this is that, at the critical point, "no energy" is required to change liquid water into steam (or vice-versa) or that the "Latent Heat of Vaporization" is 0.

The following diagram from W. J. Kearton, Steam Turbine Theory and Practice (5th ed. 1948) (comments in red have been added) shows the key feature for the system formed by liquid water and steam. This key feature applies to all critical point systems, based on the critical point principle of universality. As the system approaches the critical point from a lower temperature, the "Latent Heat of Vaporization" falls to 0 very rapidly from a high figure. I am suggesting that something like the "Latent Heat of Vaporization" is the "hook" for connecting activity patterns involving neuronal groups. With just a small upward swing in temperature, so the metaphor goes, the hook can shrink from thick to thin, allowing for easy connecting and disconnecting of the units, before the temperature drops a bit, when the hook grows thick again and the connections become fixed. I suggest that repeated upward and downward swings of a temperature-like parameter in the region just below the critical point constitutes phasic cycling, where phases are merged, then separated, then merged again.
home page (...)

site information (...)

Copyright © 2007 Robert Kovsky